Perímetro y área

Resultado de imagen para perimetro y area

Perímetro: es la suma de los lados de una figura geométrica. Es su contorno.

Ejemplos:

Los lados del rectángulo de la figura miden 10 cm. y 5 cm.

10 cm

El perímetro del rectángulo lo obtenemos sumando todos sus lados:

Perímetro = 10 cm + 5 cm + 10 cm + 5 cm = 30 cm

Por lo tanto, el perímetro del rectángulo es 30 cm.

Respecto al cuadrado , el perímetro (la longitud de su contorno) se obtiene sumando sus cuatro lados

Ver: PSU: Matematica,

Pregunta 17_2010

Pregunta 11_2005

Pregunta 05_2005Geometría

En la figura, los lados del triángulo miden 4 m.

Para obtener el perímetro sumamos sus lados:

Perímetro = 4 m + 4 m + 4 m = 12 m

El perímetro del triángulo es 12 m

Área: es la medida de la superficie de una figura; es decir, la medida de su región interior.

Área de un rectángulo

El área del rectángulo corresponde a la medida de la región verde, y se obtiene multiplicando la base por la altura.

Área = base · altura

Ejemplo:

Los lados del rectángulo de la figura miden 10 cm. y 5 cm.

10 cm	La altura de este rectángulo mide 5 cm.

10 cm	La base de este rectángulo mide 10 cm.

Área = 10 · 5 = 50 cm 2

el área del rectángulo es 50 cm 2

El centímetro cuadrado (cm 2 ) es una unidad que nos permite medir áreas. También pueden ser metros cuadrados (m 2 ), milímetros cuadrados (mm 2 ), etc.

Área del cuadrado

El área de un cuadrado es igual al producto de lado por lado.

Área de un triángulo

El área de un triángulo es igual a la mitad de su base por la altura.

Ejemplos:

Si la base de un triángulo mide 10 cm y su altura mide 5 cm., entonces el área del triángulo es 25 cm 2

POLIGONOS

En primer lugar veremos lo relacionado con los polígonos.

El perímetro de un polígono es igual a la suma de las longitudes de sus lados y su área es la medida de la región o superficie encerrada por un polígono.

2- Área y perímetro del triángulo

- Cálculo del perímetro

Es la longitud de su contorno ó la suma de sus lados.

P = a + b + c

EJEMPLOS:

Obtener el perímetro y el área de las figuras que se mencionan en los siguientes casos.

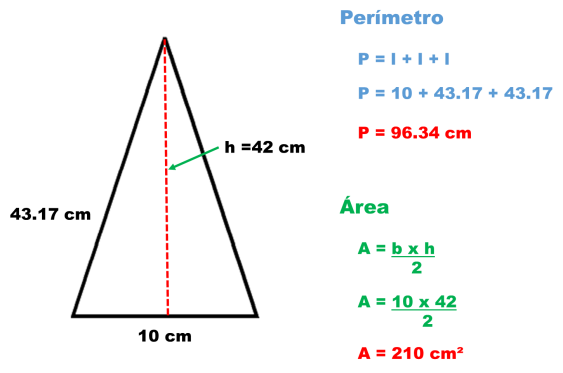
1.- Un triángulo cuya base mide 10 cm, su lado 43.17 cm y su altura 42 cm

2.- Una mesa cuadrada de 1.20 m de lado.

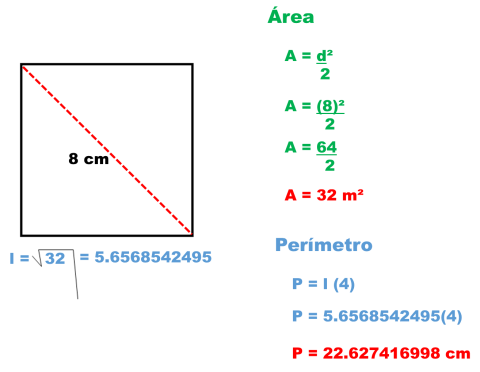
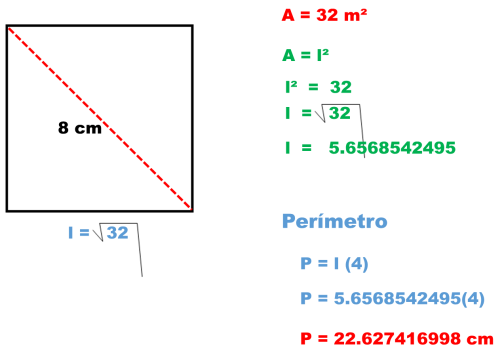
3.- Una superficie cuadrada cuya diagonal mide 8 cm.

Al conocer su área puedo obtener la medida de su lado al extraer raíz cuadrada a 32 que es 5.6568542495

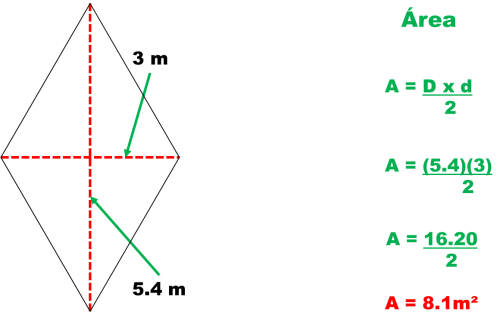
4.- Un rombo cuyas diagonales miden 5.4 cm y 3cm.

Con los datos conocidos puedo obtener el área.

Para saber la medida de su lado utilizo el Teorema de Pitágoras y así poder obtener el perímetro. Aproximadamente el lado mide 3.088 cm

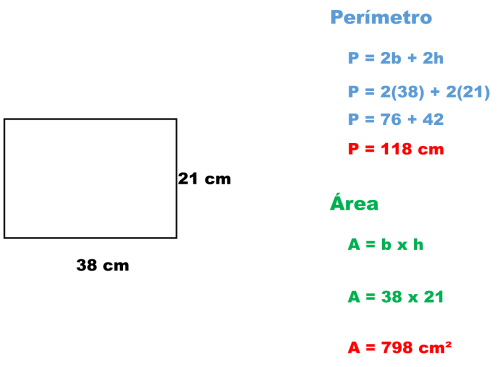
5.- Una tapa de zapatos que mide 38 cm de largo por 21 cm de ancho.

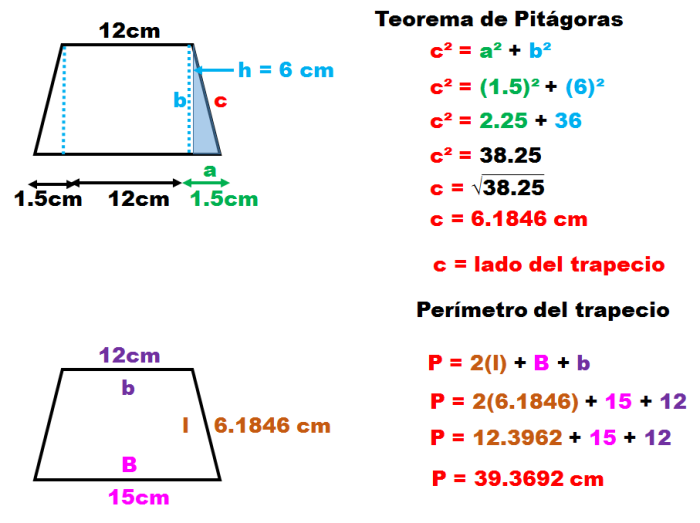
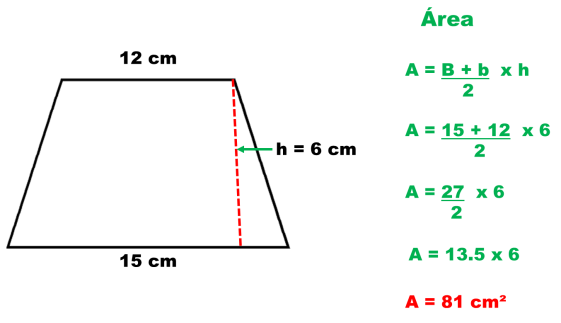
6.- Un trapecio cuyas bases miden 12 y 15 cm y de altura mide 6 cm

Al trazar el trapecio con las medidas conocidas, puedo saber la medida de su lado utilizando el Teorema de Pitágoras para obtener el perímetro.

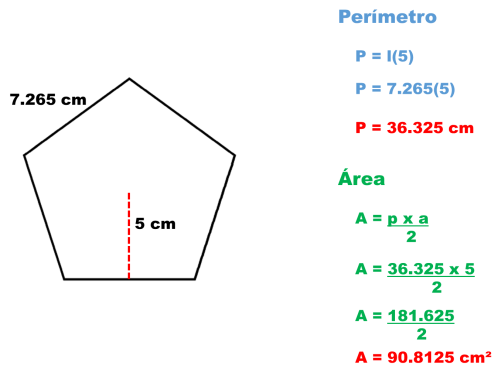
7.- Un pentágono regular que mide 7.265 cm de lado y 3 cm de apotema.

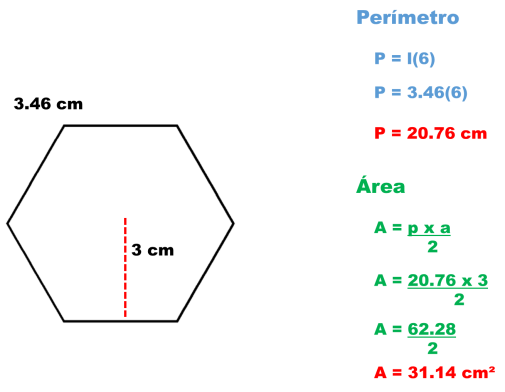
8.- Un hexágono regular de 3.46 cm de lado y 3 cm de apotema.

9.- Un círculo cuyo diámetro mide 6 cm

Te proporciono un formulario para obtener perímetros y áreas.

VIDEOS:

-https://www.youtube.com/watch?v=ckthOYdBgnc

-https://www.youtube.com/watch?v=h-hiBtE_CVA

-https://www.youtube.com/watch?v=X0f7GW0wVJM

-https://www.youtube.com/watch?v=KTzyfHvsEdc

Función definida a trozos

En matemáticas, una función segmentada (también denominada función por ,función seccionada o función definida por tramos) es una función cuya definición, (la regla que define la dependencia), llamada regla de correspondencia, cambia dependiendo del valor de la variable independiente.¹

Formalmente, una función real f (definida a trozos) de una variable real x es la relación cuya definición está dada por varios conjuntos disjuntos de su dominio (conocidos como subdominios).

La palabra "A trozos" se usa para describir cualquier propiedad de una función definida a trozos que se cumple para cada trozo aunque podría no cumplirse para todo el dominio de f. Por ejemplo, una función es diferenciable a trozos si cada trozo es diferenciable a lo largo del dominio. En análisis convexo, la noción de la derivada puede ser reemplazada por la de partes subderivada para funciones definidas a trozos.

Definición

Si A y B son dos conjuntos cualesquiera y f una función

$f:A\to B$ $f:A\to B$

definida entre ellos. Supongamos que A puede representarse como una unión de conjuntos disjuntos A_i

$A=\bigcup _{i=1}^{n}A_{i},\quad {\mbox{ con }}A_{i}\cap A_{j}=\emptyset \ \forall j\neq i$ $A=\bigcup _{i=1}^{n}A_{i},\quad {\mbox{ con }}A_{i}\cap A_{j}=\emptyset \ \forall j\neq i$

y que, para cada uno de los A_i, existe una función f_i

$f_{i}:A_{i}\to B$ $f_{i}:A_{i}\to B$

Entonces

f es una función definida a trozos si $\forall x\in A_{i}\ f(x)=f_{i}(x),\quad 1\leq i\leq n$ $\forall x\in A_{i}\ f(x)=f_{i}(x),\quad 1\leq i\leq n$ .

En otras palabras, f es definida a trozos si su regla de asignación es diferente para al menos dos valores de la variable independiente.

Notación e interpretación

Gráfica de la función valor absoluto, y = |x|.

Las funciones definidas a trozos se expresan con una notación funcional común, donde el cuerpo de la función es una lista de expresiones matemáticas asociadas a subconjuntos del dominio.

Por ejemplo, la función valor absoluto

\mathrm {abs} :\mathbb {R} \longrightarrow \mathbb {R}

puede definirse así

|x|\equiv \mathrm {abs} \,(x)=\left\{{\begin{array}{rcl}-x,&{\mbox{si }}&x<0\\x,&{\mbox{si }}&x\geq 0\end{array}}\right.

En este caso, el dominio fue dividido en los conjuntos

$D_{1}=\{x\in \mathbb {R} :x<0\},\quad D_{2}=\{x\in \mathbb {R} :x\geq 0\}$ $D_{1}=\{x\in \mathbb {R} :x<0\},\quad D_{2}=\{x\in \mathbb {R} :x\geq 0\}$

los cuales son disjuntos y cumplen

$D_{1}\cup D_{2}=\mathbb {R}$ $D_{1}\cup D_{2}=\mathbb {R}$

Para todos los valores de x menores que cero, la primera expresión matemática de la definición de abs(x) debe ser utilizada. Como esta expresión es –x, el signo del valor que asignamos a la variable independiente se invierte. De modo similar, para todos los valores de x mayores o iguales que cero, la segunda expresión matemática (la función x) es utilizada.

A continuación, se presenta una tabla con valores de abs(x), en algunos puntos x del dominio.

x	abs(x)	Expresión utilizada
−3	3	−x
−0.1	0.1	−x
0	0	x
1/2	1/2	x
5	5	x

En general, para evaluar una función definida a trozos en un determinado valor del dominio, seleccionamos la expresión matemática cuyo subdominio contiene el valor a evaluar.

Continuidad

Una función definida a trozos es continua en un intervalo dado si está definida por el intervalo, las expresiones matemáticas apropiadas que constituyen a la función son continuas en ese intervalo, y no hay discontinuidad en ningún punto extremo de los subdominios en ese intervalo.

La función que está a la derecha, por ejemplo, es una función definida a trozos continua en todos sus subdominios, pero no es continua en todo el dominio. Dicha función tiene un salto de discontinuidad (un agujero) en

x_{0}

QUÉ HACER

En la primera escena puedes ver la gráfica de la función definida según la fórmula

con valores iniciales de los deslizadores a = -0.5, b = 1, c = -1, es decir, la gráfica que se ve es:

La primera parte de la actividad consiste en el estudio de las propiedades fundamentales de esta función en lo referido a su dominio, continuidad, crecimiento y decrecimiento y máximos y mínimos.

Después analizarás cuáles han de ser los valores de los parámetros para que la función sea continua.

En la segunda parte de la actividad resolvererás ejercicios de este mismo tipo en los que tú tendrás que dibujar la gráfica.

EJEMPLOS: