En matemáticas, las funciones trigonométricas son las
funciones establecidas con el fin de extender la definición de las razones
trigonométricas a todos los números reales y complejos.
Las funciones trigonométricas son de gran importancia en
física, astronomía, cartografía, náutica, telecomunicaciones, la representación
de fenómenos periódicos, y otras muchas aplicaciones.
Conceptos básicos
Las funciones trigonométricas se definen comúnmente como el
cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las
funciones trigonométricas son funciones cuyos valores son extensiones del
concepto de razón trigonométrica en un triángulo rectángulo trazado en una
circunferencia unitaria (de radio unidad). Definiciones más modernas las
describen como series infinitas o como la solución de ciertas ecuaciones
diferenciales, permitiendo su extensión a valores positivos y negativos, e
incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas
cuatro, se definen en relación de las dos primeras funciones, aunque se pueden
definir geométricamente o por medio de sus relaciones. Algunas funciones fueron
comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan
actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo:
{\displaystyle \alpha } \alpha , del
vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este
ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los
sucesivo será:
La hipotenusa (h) es el lado opuesto al ángulo recto, o lado
de mayor longitud del triángulo rectángulo.
El cateto opuesto (a) es el lado opuesto al ángulo
{\displaystyle \alpha } \alpha .
El cateto adyacente (b) es el lado adyacente al ángulo {\displaystyle
\alpha } \alpha .
Todos los triángulos considerados se encuentran en el Plano
Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o
180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos
se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a
continuación definen estrictamente las funciones trigonométricas para ángulos
dentro de ese rango:
1) El seno de un ángulo es la relación entre la longitud del
cateto opuesto y la longitud de la hipotenusa:
El valor de esta relación no depende del tamaño del
triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo
{\displaystyle \alpha } \alpha , en cuyo caso se trata de triángulos
semejantes.
2) El coseno de un ángulo es la relación entre la longitud
del cateto adyacente y la longitud de la hipotenusa:
3) La tangente de un ángulo es la relación entre la longitud
del cateto opuesto y la del adyacente:
4) La cotangente de un ángulo es la relación entre la
longitud del cateto adyacente y la del opuesto:
5) La secante de un ángulo es la relación entre la longitud
de la hipotenusa y la longitud del cateto adyacente:
6) La cosecante de un ángulo es la relación entre la
longitud de la hipotenusa y la longitud del cateto opuesto:
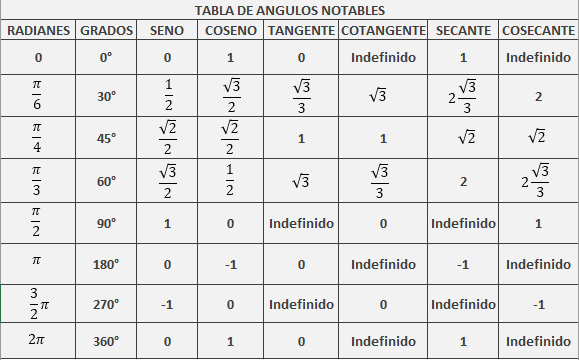
Definición para un número real cualquiera
No es posible utilizar la definición dada anteriormente, un
coseno de {\displaystyle \alpha } \alpha
para valores de {\displaystyle \alpha } \alpha menores o iguales a 0 o valores mayores o
iguales a π/2, pues no se podría construir un triángulo rectángulo tal que uno
de sus ángulos mida {\displaystyle \alpha } \alpha radianes. Para definir los valores de estas
funciones para valores comprendidos entre 0 y 2π, se utilizará entonces una
circunferencia unitaria, centrada en el origen de coordenadas del plano
cartesiano. Se definirán las funciones trigonométricas seno y coseno como la
abscisa y la ordenada, respectivamente, de un punto P perteneciente a la
circunferencia, siendo {\displaystyle \alpha } \alpha el ángulo, medido en radianes, entre el
semieje positivo x y el segmento que une el origen con P.
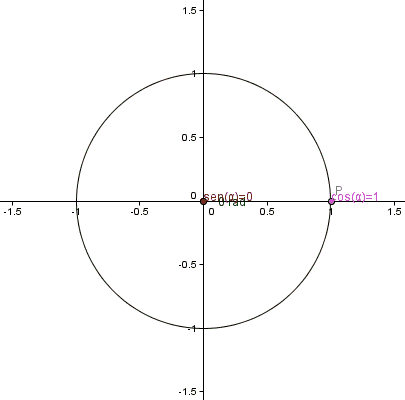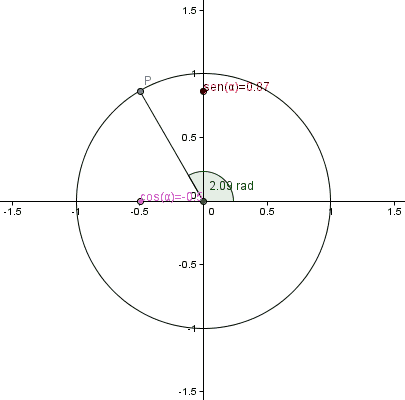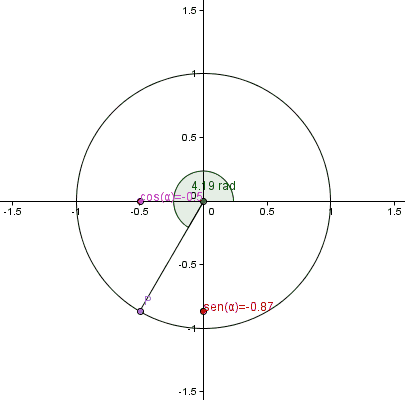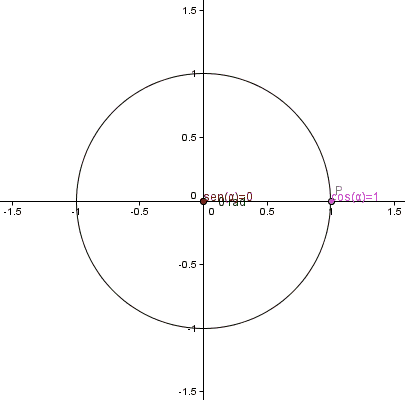
Puede
observarse que estas funciones toman valores entre -1 y 1. Nótese que para
valores entre 0 y π/2, los valores obtenidos para el seno y el coseno con esta
definición, coinciden con los obtenidos utilizando la noción de razón trigonométrica.
Si el valor de x está fuera del intervalo [0,2π], puede descomponerse como
x=2kπ+x' siendo k un número entero y x' un valor entre 0 y 2π. Se asignará a x
los mismos valores de seno y coseno que los asignados a x', ya que puede
interpretarse a x como un ángulo coterminal con x', y por lo tanto, las
coordenadas del punto P serán las mismas en ambos casos.
EJEMPLOS
Funciones trigonométricas ejercicios resueltos
2 Años Ago
 Antes de presentarte funciones trigonométricas ejercicios resueltos primero daremos una breve repasada al tema.
Antes de presentarte funciones trigonométricas ejercicios resueltos primero daremos una breve repasada al tema.
Las funciones trigonométricas en el plano cartesiano se describen como relaciones entre los lados de un triángulo rectángulo (triángulo en el cual uno de sus ángulos es recto).
Si el triángulo tiene un ángulo agudo θ se pueden encontrar seis razones entre las longitudes de los lados a,b y c del triángulo.
b/c, a/c, b/a, a/b, c/a, c/b
Estas relaciones dependen del ángulo θ y no del tamaño del triángulo. Si dos triángulos tienen ángulos iguales son semejantes y sus lados son proporcionales.
Las relaciones son funciones de θ y se les llama funciones trigonométricas. Las funciones trigonométricas son: seno, coseno, tangente, cotangente, secante y cosecante, sus símbolos respectivamente son: sen, cos, tan, cot, sec y csc.
Si θ es el ángulo agudo del triángulo rectángulo entonces:
Sen θ = b/c
Cos θ = a/c
Tan θ = b/a
Cot θ = a/b
Sec θ = c/a
Csc θ = c/b
Funciones trigonométricas EJERCICIOS RESUELTOS
Para que puedas saber mejor si ya entendiste el tema o necesitas practicar más con funciones trigonométricas ejercicios resueltos, primero te pondré todos los ejercicios y al final la solución para que primero intentes resolverlo tu solo y después compruebes tus resultados.
Calcule los valores de las seis funciones trigonométricas del ángulo θ:
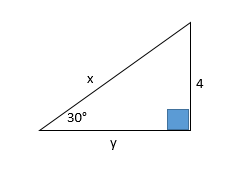
Calcule los valores de x y y
sen 30° = 4/x
sen 30° = 1/2
4/x = 1/2
x = 8
cos 30° = y / x
cos 30° = .86
y / x = y / 8 = .86
y = 6.9
sen 45 ° = 7/x
sen 45° = .70
7/x = .7
x = 9.9
cos 45° = y/x
cos 45° = .7
y/x = y/9.9 = .7
y= 7
Calcule los valores de las funciones trigonométricas del ángulo θ
7. sen θ = 3/5
8. tan θ = 5/2
SOLUCIONES:
Calcule los valores de las seis funciones trigonométricas del ángulo θ:
Sen θ = 4/5
Cos θ = 3/5
Tan θ = 4/3
Cot θ = 3/4
Sec θ = 5/3
Csc θ = 5/4
a2 + 22 = 52
Sen θ = 2/5
Csc θ = 5/2
a2 + b2 = c2
Tan θ = a/b
Cot θ = b/a
a2 + b2 = c2
Sen θ = b/c
Csc θ = c/b
Calcule los valores de x y y
Calcule los valores de las funciones trigonométricas del ángulo θ
7. sen θ = 3/5
b = 3
c = 5
a = 4
Sen θ = 3/5
Cos θ = 4/5
Tan θ = 3/4
Cot θ = 4/3
Sec θ = 5/4
Csc θ = 5/3
8. tan θ = 5/12
b = 5
a = 12
c = 13
Sen θ = 5/13
Cos θ = 12/13
Tan θ = 5/12
Cot θ = 12/5
Sec θ = 13/12
Csc θ = 13/5
EJERCICIOS:





No hay comentarios.:
Publicar un comentario