Probabilidad

La probabilidad es simplemente qué tan posible es que ocurra un evento determinado.

Cuando no estamos seguros acerca del resultado de un evento, podemos hablar acerca de la probabilidad de ciertos resultados: qué tan probables son. Al análisis de los eventos gobernados por la probabilidad se le llama estadística.

El mejor ejemplo para entender la probabilidad es echar un volado:

Hay dos posibles resultados: águila o sol.

¿Cuál es la probabilidad de que caiga águila? La podemos encontrar al usar la ecuación $P(A) = ?$ y tal vez, intuitivamente, sepas que la probabilidad es mitad y mitad, o 50%.  ¿Pero cómo podemos resolver eso?  Probabilidad = 

En este caso:

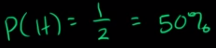
Probabilidad de un evento = (# de maneras en las que puede suceder) / (número total de resultados)

P(A) = (# de maneras en las que puede suceder A) / (número total de resultados)

Ejemplo 1

Hay seis resultados distintos.

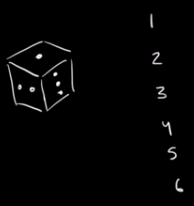
¿Cuál es la probabilidad de sacar un uno?

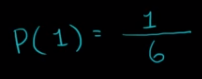
¿Cual es la probabilidad de sacar un uno o un seis?

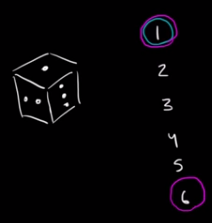
Usando la fórmula de arriba:

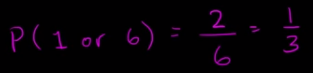
¿Cuál es la probabilidad de sacar un número par (es decir, sacar un dos, un cuatro o un seis)?

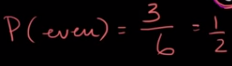
Consejos

• La probabilidad de un evento solo puede ser un número entre 0 y 1 y también puede escribirse como un porcentaje.
• La probabilidad del evento $A$ suele escribirse como $P(A)$.
• Si $P(A) > P(B)$, el evento $A$ tiene una mayor probabilidad de ocurrir que el evento $B$.
• Si $P(A) = P(B)$, los eventos $A$ y $B$ tienen la misma probabilidad de ocurrir.

EJERCICIOS:

1

Hallar:  

1

2

3

4

5

6

7

Solución

2Sean A y B dos sucesos aleatorios con:

Hallar:

1

2

3

4

Solución

3Se sacan dos bolas de una urna que se compone de una bola blanca, otra roja, otra verde y otra negra. Escribir el espacio muestral cuando:

1La primera bola se devuelve a la urna antes de sacar la segunda.

2La primera bola no se devuelve.

Solución

4Una urna tiene ocho bolas rojas, 5 amarilla y siete verdes. Si se extrae una bola al azar calcular la probabiliidad de:

1Sea roja.

2Sea verde.

3Sea amarilla.

4No sea roja.

5No sea amarilla.

Solución

5Una urna contiene tres bolas rojas y siete blancas. Se extraen dos bolas al azar. Escribir el espacio muestral y hallar la probabilidad de los sucesos:

1Con reemplazamiento.

2Sin reemplazamiento.

Ejercicio 1

Sean A y B dos sucesos aleatorios con:

Hallar:  

1

2

3

4

5

6

7

Ejercicio 2

Sean A y B dos sucesos aleatorios con:

Hallar:

1

2

3

4

Ejercicio 3

Se sacan dos bolas de una urna que se compone de una bola blanca, otra roja, otra verde y otra negra. Escribir el espacio muestral cuando:

1La primera bola se devuelve a la urna antes de sacar la segunda.

E = {BB, BR, BV, BN, RB, RR, RV, RN, VB, VR, VV, VN, NB, NR, NV, NN}

2La primera bola no se devuelve.

E = { BR, BV, BN, RB, RV, RN, VB, VR, VN, NB, NR, NV}

Ejercicio 4

Una urna tiene ocho bolas rojas, 5 amarilla y siete verdes. Si se extrae una bola al azar calcular la probabiliidad de:

1Sea roja.

2Sea verde.

3Sea amarilla.

4No sea roja.

5No sea amarilla.

Ejercicio 5

Una urna contiene tres bolas rojas y siete blancas. Se extraen dos bolas al azar. Escribir el espacio muestral y hallar la probabilidad de los sucesos:

1Con reemplazamiento.

2Sin reemplazamiento.